30 大编程面试问题 (2025)

30 大编程面试问题 (2025)

科技
admin

如果您作为新手或经验丰富的人来申请软件开发人员的角色，那么您必须熟悉编程概念的核心，并能够编写干净、健壮的代码，这一点至关重要。

在本文中，您将遇到一些最常见的面试问题，包括有关数据结构（数组、字符串、链表、树、图等）和算法（排序、搜索、递归、动态编程、 ETC）。

如果你在这里，那就意味着你的战斗已经成功了一半！因此，无需进一步说明，让我们深入了解吧！

目录

题库

1.什么是数据结构？ C++中有哪些数据结构？

数据结构是一种以某种格式存储数据以进行计算或操作的方法。

C++ 中一些重要的数据结构是 –

  • 数组
  • 哈希映射
  • 链表
  • 树木
  • 图表

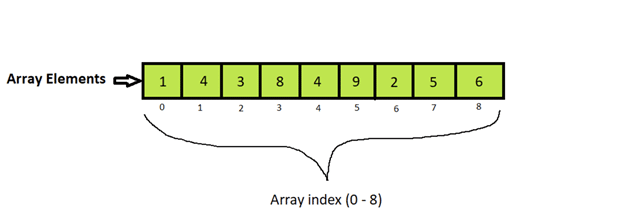
2. 数组与链表有何不同？

数组和链表是存储一组值的线性数据结构。然而，它们仍然有很大不同。我们来详细了解一下。

大批

  • 有固定尺寸
  • 需要连续的内存分配
  • 任何元素都可以直接访问，时间复杂度为 O(1)
  • 除了存储值之外不需要额外的存储空间
  • 当数据结构的大小必须固定时建议使用

数组元素数组元素

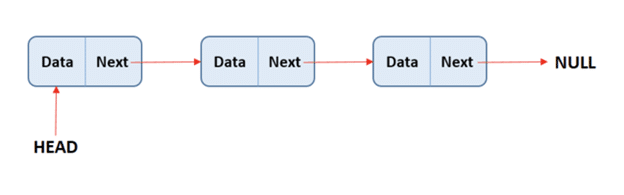
链表

  • 尺寸各异
  • 分配的内存可以是不连续的或分散的
  • 需要额外的内存空间来存储指针
  • 任何元素都可以通过遍历完整链表来访问，时间复杂度为 O(n)。
  • 建议在数据结构大小可以改变的情况下使用

链表链表

3. 编写一段代码来查找数组中的第二大元素？

查找数组中第二大元素的代码如下 –

function findSecondLargest(arr) {
    let first = -Infinity, second = -Infinity;
    for (let num of arr) {
        if (num > first) {
            second = first;
            first = num;
        } else if (num > second && num < first) {
            second = num;
        }
    }
    return second;
}

console.log(findSecondLargest([3, 5, 1, 10, 4]))  ;

输出： 5

伪代码

Function findSecondLargest(arr):
# Initialize two variables to hold the largest and second largest values
first = -Infinity
second = -Infinity

# Loop through each element in the array
FOR num in arr:
IF num > first:
# Update second to hold the previous largest value
second = first
# Update first to the new largest value
first = num
ELSE IF num > second AND num < first:
# Update second if num is greater than second but less than first
second = num

# Return the second largest value
RETURN second

4.什么是堆栈？举例说明如何使用它们？

堆栈被称为 LIFO，即后进先出数据结构。最后进入堆栈的元素将首先被打印。可以理解为将一块板堆叠在另一块上面，然后从顶部取出它们。

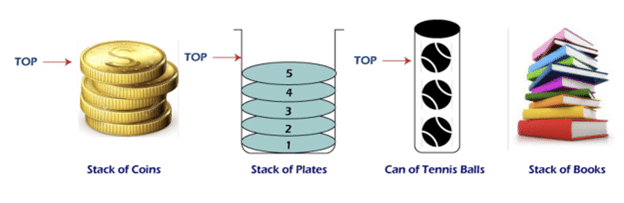
什么是堆栈什么是堆栈

在堆栈上执行的操作

  1. Push：将元素添加到栈顶
  2. Pop：将从栈顶移除元素
  3. Peek/Top：将获取元素，但不会将其从堆栈中删除
  4. isEmpty：检查堆栈是否不包含元素。它返回 true 或 false。
#include <stack> 
#include <iostream>
int main() {
    std::stack<int> stack;
    stack.push(10); // This will add 10 to the stack
    stack.push(20); // This will add 20 to the stack

    stack.push(30); // This will add 30 to the stack

    std::cout << "Top element: " << stack.top() << "\n"; 
// This will print the top element i.e. 30

    stack.pop(); //  This will remove 30 from the stack’s top

    std::cout << "Top element after pop: " << stack.top() << "\n"; 
//  This will print 20
    return 0;
}

5.什么是队列？举例说明如何使用它们？

队列是一种遵循先进先出（First In First Out）方式的数据结构。所以先插入的元素会先出来。这就像排队时，第一个人获得第一个机会。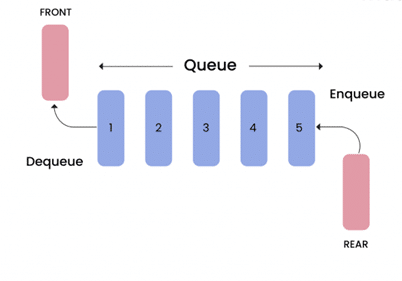
什么是队列什么是队列

对队列执行的操作

  • 入队（推送）——这将在末尾添加一个值
  • Dequeue (Pop) – 这将从前面删除值
  • Front – 这是访问队列中的第一个元素
  • isEmpty – 检查队列是否完全为空。它返回 true 或 false。
#include <queue>
#include <iostream> 
int main() {
    std::queue<int> queue;
    queue.push(10); // This will add 10 to the Queue    queue.push(20); // This will add 20 to the Queue    
    queue.push(30); // This will add 30 to the Queue    

    std::cout << "Front element: " << queue.front() << "\n"; // This will output 10
    queue.pop(); // This will remove 10
    std::cout << "Front element after pop: " << queue.front() << "\n"; // This will output 20
    return 0;
}

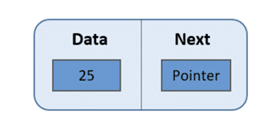
6.链表中节点的结构是什么？

链表基本上是一组节点。每个节点存储数据和指向下一个节点的指针。

每个音符的结构如下所示 –

节点的结构节点的结构

struct Node {
    int data;
    Node* next;
};

7. 编写一段代码来反转链表。

反转链表的代码如下：

	function reverseLinkedList(head) {
    let prev = null, current = head;
    while (current) {
        let next = current.next;
        current.next = prev;
        prev = current;
        current = next;
    }
    return prev;
}

8. 什么是Floyd’s Cycle检测算法？编写相同的代码。

function hasCycle(head) {
    let slow = head, fast = head;
    while (fast && fast.next) {
        slow = slow.next;
        fast = fast.next.next;
        if (slow === fast) return true;
    }
    return false;
}

解释： 此函数使用弗洛伊德循环检测算法（龟兔赛跑方法）检测链表中是否存在循环。

  1. 有两个指针——慢速和快速
    • 缓慢地一步一步地移动。
    • 一次快速移动两步。
  2. 如何检测循环？

如果存在循环，快指针最终会在某个节点与慢指针相遇，慢指针将返回 true。

  • 但是，如果不存在循环，fast 或 fast.next 将达到 null，并且该函数将返回 false

您的 Web 开发精通之旅从这里开始！

今天报名，改变你的未来！

测验图标测验图标



9. 如何使用两个队列实现堆栈？

实现具有两个队列的堆栈的代码如下-

class Stack {
    constructor() {
        this.q1 = [];
        this.q2 = [];
    }
    push(x) {
        this.q1.push(x);
    }
    pop() {
        while (this.q1.length > 1) {
            this.q2.push(this.q1.shift());
        }
        let popped = this.q1.shift();
        [this.q1, this.q2] = [this.q2, this.q1];
        return popped;
    }
}

10.什么是树？

树是一种由节点组成的数据结构。树中的每个节点都有指向其子节点的指针。它是一种用于表示关系的非线性结构。

一棵树有一个根节点，它是树的入口点，也是主节点。它有各种称为叶节点的子节点。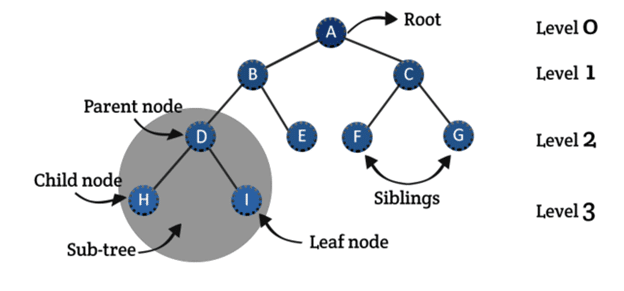
什么是树什么是树

11. 遍历一棵树有哪两种方式？

可以使用以下方式遍历一棵树 BFS（广度优先搜索） 或者 DFS（深度优先搜索）。

在 广度优先遍历 树是逐层遍历的，这意味着在进入下一层之前，首先访问某一层的所有节点。

在 深度优先遍历 树的一个分支会遍历到最底部，然后回溯并到达下一个分支。

DFS 可以通过三种方式完成 –

  • 中序遍历 – 在此，我们访问左子树，然后返回到根，然后返回右子树。
  • 前序遍历——首先我们访问根，然后访问左子树，然后访问右子树。
  • 后序遍历 – 在此，我们访问左子树，然后访问右子树，然后访问根。

12.

1
/\
2 3
/\
4 5

对于给定的二叉树，写下以下的遍历输出：

1.有序
2. 预购
3. 邮购
4. 等级顺序

输出如下 –

  1. 顺序 – 4 2 5 1 3
  2. 预购 – 1 2 4 5 3
  3. 邮购 – 4 5 2 3 1
  4. 等级顺序 – 1 2 3 4 5

13. 编写代码实现快速排序。

function quickSort(arr) {
    if (arr.length <= 1) return arr; let pivot = arr[arr.length - 1]; let left = arr.filter(el => el < pivot); let right = arr.filter(el => el > pivot);
    return [...quickSort(left), pivot, ...quickSort(right)];
}

console.log(quickSort([3, 6, 1, 8, 4]));

输出-

[1, 3, 4, 6, 8]

14. 如何检查字符串是否是回文？

笔记： 回文字符串是一种向前和向后读取相同的字符串。

示例——女士

#include <iostream>
using namespace std;

bool isPalindrome(string str) {
    int start = 0;
    int end = str.length() - 1;

    while (start < end) {
        if (str[start] != str[end])
            return false;
        start++;
        end--;
    }
    return true;
}
int main() {
    string str = "racecar";

    if (isPalindrome(str))
        cout << str << " is a palindrome." << endl;
    else
        cout << str << " is not a palindrome." << endl;

    return 0;
}

15. 编写一段代码来检查两个字符串是否是字谜词。

笔记： 如果两个字符串以不同或相同的顺序包含相同频率的相同字符，则它们是字谜词。

例子： 倾听并保持沉默

#include <iostream> 
#include <algorithm> 
using namespace std;

bool areAnagrams(string str1, string str2) {
    // If the lengths of two strings are different, they cannot be anagrams
    if (str1.length() != str2.length())
        return false;

    // Sort both strings
    sort(str1.begin(), str1.end());
    sort(str2.begin(), str2.end());

    // Compare sorted strings
    return str1 == str2;
}

int main() {
    string str1 = "listen";
    string str2 = "silent";

    if (areAnagrams(str1, str2))
        cout << "The strings are anagrams." << endl;
    else
        cout << "The strings are not anagrams." << endl;

    return 0;
}

16. 编写代码来交换两个数字而不使用第三个数字。

#include <iostream>
using namespace std;

int main() {
    int a = 5, b = 10;

    cout << "Before swapping: a = " << a << ", b = " << b << endl;

    a = a + b; // a now becomes 15
    b = a - b; // b becomes 5 (original a)
    a = a - b; // a becomes 10 (original b)

    cout << "After swapping: a = " << a << ", b = " << b << endl;

    return 0;
}

17.什么是递归？

递归是一个函数不断调用自身直到到达基本情况并从那里返回一个值到顶部的过程。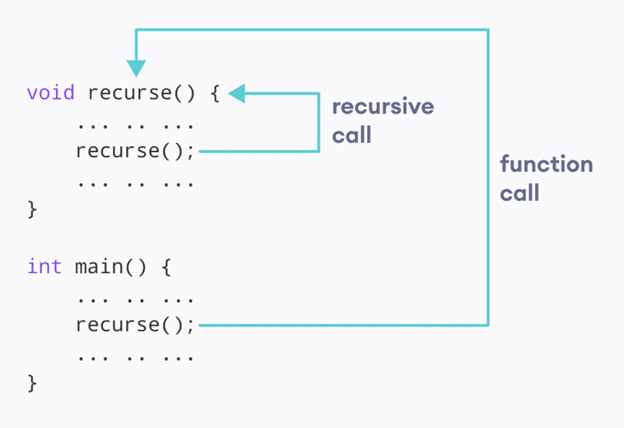
什么是递归什么是递归

18. 使用递归计算阶乘？

#include <iostream>
using namespace std;

int factorial(int n) {
    if (n == 0 || n == 1)  // Base case: 0! = 1 and 1! = 1
        return 1;
    return n * factorial(n - 1);  // Recursive case
}

int main() {
    int num = 5;
    cout << "Factorial of " << num << " is " << factorial(num) << endl;
    return 0;
}

19. 编写一段高效的代码来反转单链表。

function reverseLinkedList(head) {
    let prev = null, current = head;
    while (current) {
        let next = current.next;
        current.next = prev;
        prev = current;
        current = next;
    }
    return prev;
}

释放您的 Web 开发潜力！

现在加入，开始构建您的梦想项目！

测验图标测验图标



20. 编写代码检查二叉树是否平衡？

function isBalanced(root) {
    function height(node) {
        if (!node) return 0;
        let left = height(node.left);
        let right = height(node.right);
        if (Math.abs(left - right) > 1) return -1;
        return Math.max(left, right) + 1;
    }
    return height(root) !== -1;
}

21.什么是OOP概念？

OOP 代表 面向对象编程。这是一组帮助用户编写标准、模块化和可重用代码的概念。

面向对象编程有四个概念——

  • 抽象 – 抽象是指向用户隐藏复杂数据并显示对开发人员和用户有用的数据的过程。
  • 封装 – 这是将数据和方法捆绑到称为类的单个单元中的过程。通过这样做，我们可以限制其他组件对数据的访问，从而创建一个安全层。
  • 遗产 – 继承是子类可以访问父类的方法和属性的过程。
  • 多态性 – 多态是单个函数表现出不同特征并执行不同角色的过程。

22.什么是二叉搜索树？它的主要特点是什么？

50

/\

30 70

/ \ / \

20 40 60 80

二叉搜索树是二叉树的变体。在这棵树中，左侧每个节点的值都小于根/父节点，右侧每个节点的值都大于根/父节点。

特征 –

  • 二叉树中的每个节点最多可以有两个子节点
  • 搜索、插入和删除等操作的时间复杂度为 O(logn)。

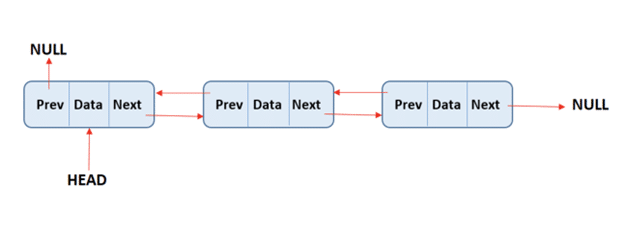
23.什么是双向链表？

双向链表是链表数据结构的一种变体，包含以下内容 –

  • 每个节点存储一些需要处理的数据
  • 它包含一个指向下一个节点的指针
  • 它还包含指向前一个节点的指针

双向链表双向链表

24. 编写代码以在图中执行深度优先搜索。

我们可以按照下面代码中的方式在图中执行深度优先搜索：

#include <iostream>
#include <vector>
using namespace std;

void dfs(int node, vector<int> adj[], vector<bool>& visited) {
    visited[node] = true;
    cout << node << " ";

    for (auto neighbor : adj[node]) {
        if (!visited[neighbor]) {
            dfs(neighbor, adj, visited);
        }
    }
}

int main() {
    int V = 5;
    vector<int> adj[V];
    vector<bool> visited(V, false);

    // Adding edges
    adj[0] = {1, 4};
    adj[1] = {0, 2, 3, 4};
    adj[2] = {1, 3};
    adj[3] = {1, 2, 4};
    adj[4] = {0, 1, 3};

    cout << "DFS Traversal: ";
    dfs(0, adj, visited);
    cout << endl;

    return 0;
}

25. 编写一段代码来查找未加权图中的最短路径。

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

void shortestPath(int src, vector<int> adj[], int V) {
    vector<int> dist(V, -1);
    queue<int> q;

    q.push(src);
    dist[src] = 0;

    while (!q.empty()) {
        int node = q.front();
        q.pop();

        for (auto neighbor : adj[node]) {
            if (dist[neighbor] == -1) {
                dist[neighbor] = dist[node] + 1;
                q.push(neighbor);
            }
        }
    }

    cout << "Shortest distances from node " << src << ": ";
    for (int i = 0; i < V; i++) {
        cout << dist[i] << " ";
    }
    cout << endl;
}

int main() {
    int V = 5;
    vector<int> adj[V];

    adj[0] = {1, 4};
    adj[1] = {0, 2, 3, 4};
    adj[2] = {1, 3};
    adj[3] = {1, 2, 4};
    adj[4] = {0, 1, 3};

    shortestPath(0, adj, V);

    return 0;
}

26.你对HashMap有什么理解？编写代码以使用 HashMap 查找数组中两个元素的总和。

HashMap 是一种存储键值对的数据结构。它允许高效地检索、插入和删除数据。

哈希映射哈希映射

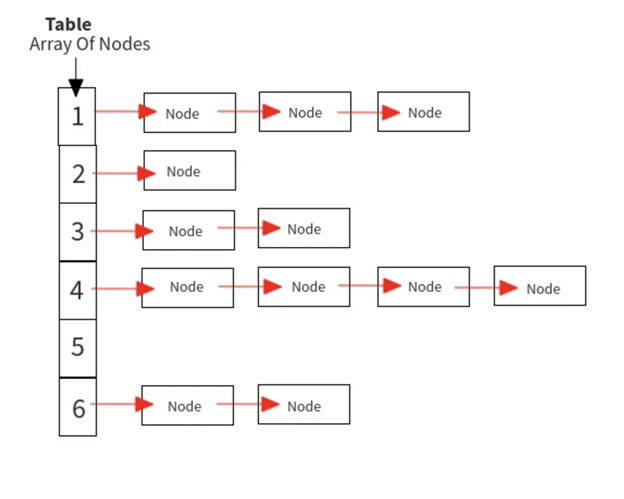
使用 Hashmap 求数组中两个元素之和的代码如下：

#include <iostream>
#include <unordered_map>
#include <vector>
using namespace std;

vector twoSum(vector& nums, int target) {
    unordered_map<int, int> numMap; // Value -> Index mapping
    vector result;

    for (int i = 0; i < nums.size(); i++) {
        int complement = target - nums[i];
        if (numMap.find(complement) != numMap.end()) {
            result.push_back(numMap[complement]);
            result.push_back(i);
            return result;
        }
        numMap[nums[i]] = i;
    }

    return result; // No solution
}

int main() {
    vector nums = {2, 7, 11, 15};
    int target = 9;

    vector result = twoSum(nums, target);

    if (!result.empty()) {
        cout << "Indices: " << result[0] << ", " << result[1] << endl;
    } else {
        cout << "No solution found." << endl;
    }

    return 0;
}

27. 编写一段代码来查找两个字符串中的最长公共子序列。另外，提到它的空间和时间复杂度。

笔记 – LCS 是在两个字符串中以相同相对顺序出现的最长序列，但不一定是连续的。

例子 – 对于字符串 ABCBDAB 和 BDCAB，LCS 是 BCAB。

#include <iostream>
#include <vector>
#include <string>
using namespace std;

string longestCommonSubsequence(string text1, string text2) {
    int m = text1.length(), n = text2.length();
    vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));

    // Fill the dp table
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            if (text1[i - 1] == text2[j - 1]) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            } else {
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }

    // Reconstruct the LCS from the dp table
    string lcs = "";
    int i = m, j = n;
    while (i > 0 && j > 0) {
        if (text1[i - 1] == text2[j - 1]) {
            lcs = text1[i - 1] + lcs;  // Include this character in LCS
            i--;
            j--;
        } else if (dp[i - 1][j] > dp[i][j - 1]) {
            i--;  // Move up in the table
        } else {
            j--;  // Move left in the table
        }
    }

    return lcs;
}

int main() {
    string str1 = "ABCBDAB";
    string str2 = "BDCAB";

    string lcs = longestCommonSubsequence(str1, str2);

    cout << "The Longest Common Subsequence is: " << lcs << endl;
    return 0;
}

28.你对时间和空间复杂性有何理解？

时间复杂度是算法完成任务所花费的时间。它被表示为使用 大 O 表示法。

  • 如果任务花费常数时间，则将其表示为 O(1)。
  • 如果任务需要对数时间，则表示为 O(log n)。
  • 如果一个任务需要线性时间，则表示为 O(n) 等等。

空间复杂度是算法在内存中占用的空间。

例如，一个数组将占用内存中的“n”个单位的空间。其中“n”是数组的大小。

29. 编写一段代码来查找句子中每个单词的出现频率。

#include <iostream>
#include <unordered_map>
#include <sstream>
using namespace std;

int main() {
    string sentence = "hello world hello everyone world";
    unordered_map<string, int> wordCount;

    // Split sentence into words and count frequencies
    stringstream ss(sentence);
    string word;
    while (ss >> word) {
        wordCount[word]++;
    }

    // Print word frequencies
    for (auto &entry : wordCount) {
        cout << entry.first << ": " << entry.second << endl;
    }

    return 0;
}

30.你对动态规划有何理解？说出它的特点和使用方法。

动态规划 (DP) 是通过将复杂问题分解为更小的可解单元来解决复杂问题的最强大技术之一。 DP的关键在于避免一次又一次地解决特定的子问题并存储其价值以供将来使用。

动态规划有两个特点——

  1. 重叠子问题：

一个较大的问题被分解为较小的问题，也称为子问题。

  1. 最优子结构：

通过解决较小的问题来解决较大的问题。

动态规划可以通过两种方式解决 –

  1. 记忆：

记忆被称为自上而下的方法。在此，我们使用递归。递归地解决问题，直到达到基本情况。

  1. 制表：

制表法被称为自下而上的方法。在这种情况下，这些值是从底部开始计算的，直到我们在顶部得到最终值。

31. 编写一段代码来查找连续数组的最大和。

int maxSubArray(vector& nums) {
int maxSum = nums[0], currentSum = nums[0];
for (int i = 1; i < nums.size(); i++) {
currentSum = max(nums[i], currentSum + nums[i]);
maxSum = max(maxSum, currentSum);
}
return maxSum;
}

解释： 函数 maxSubArray 查找给定整数数组中连续子数组的最大和。整个过程可以分为3步——

  • 初始化：
    • maxSum 和 currentSum 使用数组的第一个元素进行初始化。
  • 遍历数组：
    • 对于每个元素，将 currentSum 更新为当前元素本身的最大值或 currentSum 与当前元素的和。这有助于决定是开始一个新的子数组还是继续添加到现有的子数组。
      • 将 maxSum 更新为 maxSum 和 currentSum 中的最大值。
  • 返回结果：
    • 最后的 maxSum 表示最大子数组和。

获得 100% 的徒步旅行！

立即掌握最需要的技能！

结论

编写面试问题是展示您的技能和找到梦想工作的垫脚石。通过有效准备并保持一致，您可以充满信心地进行面试。请记住，每个问题都是学习和成长的机会。如果您想了解更多信息，您可以立即加入 Intellipaat 专家指导的编程课程，塑造您作为开发人员的职业生涯。

Related Posts

Amazon Great Indian Festival 기간 동안 최고의 노트북 제안

admin

Mostbet Online Casino Pa: Szerezze meg 10 dolláros befizetés nélküli bónuszát”

admin
브랜드 성장을 위한 6가지 강력한 TikTok 마케팅 전략

브랜드 성장을 위한 6가지 강력한 TikTok 마케팅 전략

admin