想象一下,您要从家里去大学,并希望选择最快的路径。您不会随机选择任何路线,而是会检查通往目的地的最近的转弯。这正是广度优先搜索的工作原理。
BFS 是一种图遍历算法,从我们称为源节点的选定点开始。从该源节点开始,它在移动进一步的节点之前探索其邻居,就像在进入下一层之前访问一层的所有内容一样。
目录:
数据结构中的图遍历
我们知道图是一种表示不同元素之间关系的数据结构。它由作为对象的节点和显示节点之间连接的边组成。
图遍历是一种访问图中存在的所有节点的方法。我们从一个节点开始,然后借助边探索下一个节点。
有两种不同类型的图遍历算法,允许我们以特定的顺序遍历图。
1.深度优先搜索(DFS): 它首先深入访问一个分支的所有节点,然后考虑其他节点。它使用堆栈或递归来监视节点。
2.广度优先搜索(BFS): 它首先访问同一级别中存在的所有节点,然后移动到下一个级别。
利用 BFS 算法和其他数据结构概念保持领先
访问行业领先的软件工程课程


广度优先搜索算法
广度优先搜索是一种遍历算法,它允许我们首先探索所有邻居节点,然后访问下一个邻居节点,就像先遍历一个级别然后移动到另一个级别一样。它使用队列来检查节点(顶点)。
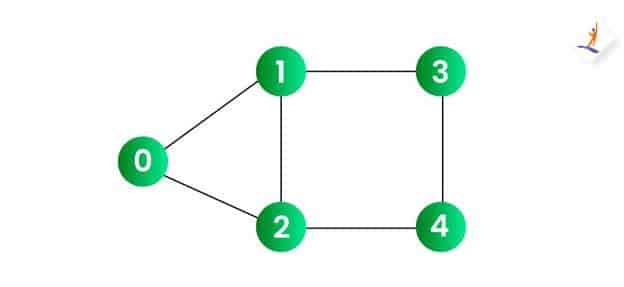
比如我们下图的起点或者说源节点是0。我们来看看BFS算法是如何遍历图的。

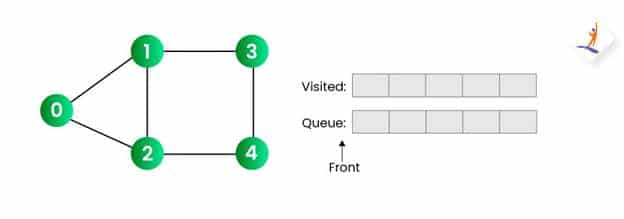
步骤一:
- 首先,我们将创建一个空队列来检查邻居节点和一个空数组来获取已访问节点的列表(已访问数组)。

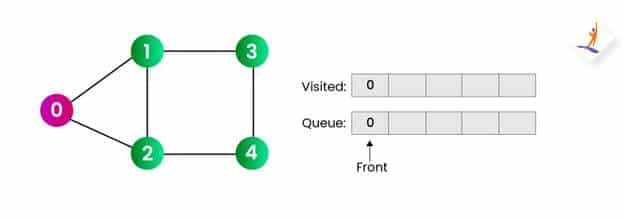
步骤2:
- 我们将把起始节点(源节点)推送到队列中,在本例中为 0。我们还将其标记为已访问。

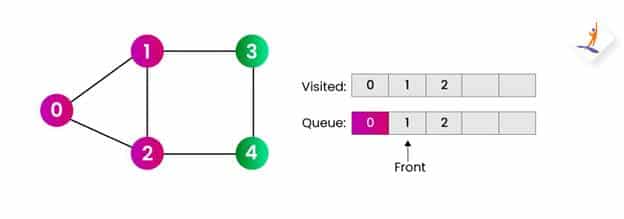
步骤3:
- 现在我们将从队列前面删除零并访问邻居节点并将它们推入队列,即 [1,2] 在我们的例子中。另外,我们会将它们添加到访问数组中。
- 我们将前端移动到节点 1

第4步:
- 现在队列中的前节点是 1。我们将推送队列中 1 的下一个邻居,并将它们也添加到访问数组中。在我们的例子中,3 是下一个邻居。
- 我们将前端移动到节点 2。
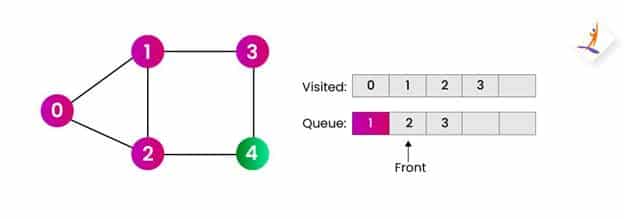

第5步:
- 现在我们将从队列中删除节点 2 并访问下一个未访问的节点。
- 将它们推入队列并将它们添加到访问数组中。
- 我们将前端移动到节点 3。
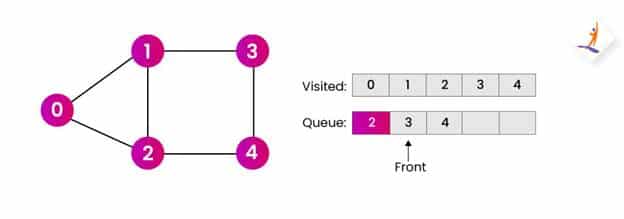

第6步:
- 现在我们将从队列中删除节点 3 并访问下一个邻居节点。
- 在我们的例子中,我们已经访问了节点 3 的所有邻居。因此,现在我们可以继续处理队列中的下一个节点。
- 我们将前端转移到节点 4
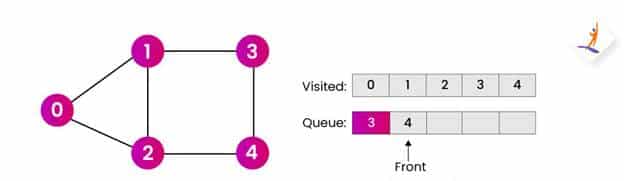

第7步:
- 最后,我们将从队列中删除节点 4 并访问邻居节点。
- 由于节点 4 没有未访问的邻居。我们不会向队列添加任何新节点。
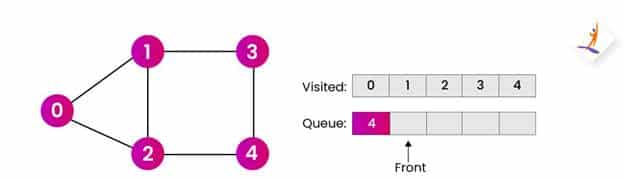

最后,我们遍历图中存在的所有节点并将它们存储在访问数组中。那是 [0,1,2,3,4]。
伪代码
下面是 BFS 函数的伪代码。
BFS(graph, start_node):1. We will create an empty queue and enqueue the start_node(source node)
2. We will mark start_node as visited
3. While the queue is not empty: ( we will perform a loop)
a. We will remove a node (current_node)
b. For each neighbor of current_node: (we will perform an inner loop)
i. If the neighbor node is not visited:
- Add it to the visited array
- Then push the neighbor into a queue
C 中的 BFS 实现
让我们看看 BFS 在 C 中的实现。
#include#include #define MAX 100 // Function to perform BFS traversal from a given starting node void bfs(int adj[MAX][MAX], int V, int start) { int queue[MAX], front = 0, rear = 0; // Queue to manage BFS traversal bool visited[MAX] = { false }; // Array to track visited nodes visited[start] = true; // Mark the starting node as visited (Bool -> True) queue[rear++] = start; // Add the starting node to the queue // Continue until the queue is empty while (front < rear) { int current = queue[front++]; // Dequeue the next node printf("%d ", current); // Print the current node // Check all vertices connected to the current node for (int i = 0; i < V; i++) { if (adj[current][i] && !visited[i]) { // If connected and not visited visited[i] = true; // Mark it as visited queue[rear++] = i; // Add it to the queue } } } } // Function to add an edge between two node in an undirected graph void addEdge(int adj[MAX][MAX], int u, int v) { adj[u][v] = adj[v][u] = 1; // Update the adjacency matrix to indicate the connection } int main() { int V = 5; // Total number of vertices in the graph int adj[MAX][MAX] = {0}; // Initialize the adjacency matrix with all zeros // Define edges in the graph addEdge(adj, 0, 1); // Add edge between vertex 0 and 1 addEdge(adj, 0, 2); // Add edge between vertex 0 and 2 addEdge(adj, 1, 3); // Add edge between vertex 1 and 3 addEdge(adj, 1, 4); // Add edge between vertex 1 and 4 addEdge(adj, 2, 4); // Add edge between vertex 2 and 4 // Perform BFS starting from vertex 0 printf("BFS starting from 0:\n"); bfs(adj, V, 0); return 0; }
输出:
从0开始的BFS:
0 1 2 3 4

广度优先搜索(BFS)算法的复杂度分析
1. BFS的时间复杂度
我们知道,在最坏的情况下,BFS 算法将至少访问图中的所有节点和边一次。这就是为什么BFS的时间复杂度是 O(V+E),这里 V 和 E 是图中的节点(顶点)和边的数量。
2. BFS的空间复杂度
由于 BFS 使用队列来跟踪我们尚未访问的节点。在最坏的情况下,队列可以存储图中的所有顶点。因此,BFS的空间复杂度为O(V)。
获得 100% 的徒步旅行!
立即掌握最需要的技能!
广度优先搜索的应用
BFS的应用如下:
- 未加权图中的最短路径:
- BFS 确保我们在未加权的图中获得起始节点和目标节点之间的最短路径。
- 例如:寻找到达餐厅的最短路径。
- 网络广播:
- BFS 在执行网络广播模拟时确保所有节点都在接收数据包。
- 例如:从一个计算机网络向另一个计算机网络发送消息。
- 检测无向图中的循环:
- 我们正在维护一个数组,使我们能够跟踪访问过的节点及其父节点。
- 搜索最小生成树:
- BFS 可以是算法(例如 Prim 算法)的一部分,用于在未加权图中查找最小生成树。
- 社交网络评估:
- BFS有助于探索用户之间的联系,这使我们能够找到两个用户之间的关系(通过检查分离度)
- 例如:在 Facebook 上寻找共同的朋友。
结论
BFS 是最简单但仍然强大的算法之一,它允许我们逐层遍历图,这使其成为在未加权图中查找最短路径的最佳算法。它是一种结构化方法,可确保按特定顺序访问每个节点,无论您是尝试解决谜题还是导航地图,都可以轻松理解图形问题。
为了加深您对 BFS 等算法的理解并增强您在软件工程领域的职业生涯,请立即报名参加我们的综合软件工程课程。



